Il y a de nombreuses façons de représenter le monde qui nous entoure. Traditionnellement, un carte représente le monde en tant qu'espace "physique" (ou plus exactement, une de ses projections) le plus fidèlement possible en termes de surfaces et distances.
Un cartogramme tente lui de représenter le monde en fonction d'une variable donnée : PIB d'un pays, densité de la population, taux d'accès à une ressource, etc. Pour ce faire, il déforme les surfaces et les distances réelles proportionnellement à la variable qu'il exprime. Cette technique est relativement récente : inventée durant le XIXème siècle, elle n'est fréquemment utilisée que depuis la seconde moitié du XXème. Par exemple, ci-dessous, la répartition des destinations touristiques dans le monde (où l'on peut voir que la France, l'Espagne et l'Italie apparaissent bien plus volumineuses que sur une carte classique de par leur forte attraction touristique). De nombreux cartogrammes sont consultables en ligne sur le site WorldMapper.
Un cartogramme tente lui de représenter le monde en fonction d'une variable donnée : PIB d'un pays, densité de la population, taux d'accès à une ressource, etc. Pour ce faire, il déforme les surfaces et les distances réelles proportionnellement à la variable qu'il exprime. Cette technique est relativement récente : inventée durant le XIXème siècle, elle n'est fréquemment utilisée que depuis la seconde moitié du XXème. Par exemple, ci-dessous, la répartition des destinations touristiques dans le monde (où l'on peut voir que la France, l'Espagne et l'Italie apparaissent bien plus volumineuses que sur une carte classique de par leur forte attraction touristique). De nombreux cartogrammes sont consultables en ligne sur le site WorldMapper.
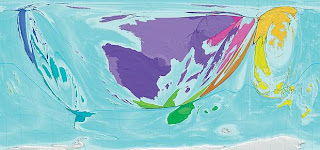
L'Atlas du monde réel (chez l'éditeur) propose avec 366 cartogrammes une représentation originale et souvent très efficace du monde, sur des problématiques très diverses (économiques, politiques, ressources, sociologiques, médicales, culturelles, etc...).
L'une des très grandes qualités de cet ouvrage (hormis sa présentation très claire et agréable) se cache derrière la méthode employée pour la génération de ses cartes. En effet, il s'agit d'une méthode numérique récente (2004) développée par Michael Gastner et Mark Newman (coauteur de l'ouvrage et chercheur numéricien à l'université du Michigan).
Cette méthode se base sur le phénomène physique de la diffusion (mécanique des fluides/thermique) : les territoires représentés se déforment comme s'il s'agissait de ballons contenant du gaz (la variable étudiée) avec des zones de pression (les zones de fortes densités de population, le plus souvent). Article de référence : Diffusion-based method for producing density equalizing maps, Michael T. Gastner and M. E. J. Newman (PDF).
D'un point de vue purement numérique, l'équation de la diffusion est résolue par une transformée de Fourrier rapide (FFT) et intégrée par une méthode de Runge-Kutta d'ordre 4. Selon les auteurs, une précision à 1.0E-4 (cela peut paraître décevant, mais une précision plus grande n'est quasiment pas observable humainement) est obtenue en peu d'itérations (ordre de temps de calcul : quelques minutes sur un ordinateur de bureau).
Ce qui m'a paru intéressant dans cette méthode, c'est l'application d'un problème de physique (la diffusion/mécanique des fluides) à un contexte tout à fait décalé (cartographie/représentation des données). Dans l'article cité plus haut, sont listées les précédentes méthodes de génération de cartogrammes, dont une autre consiste en une analogie physique avec l'élasticité des matériaux (mécanique solide déformable).
Dans d'autres domaines, pour ce type d'analogie, on peut citer l'utilisation de méthodes de CFD (calcul en mécanique des fluides) dans des calculs de trafic (routier ou autre) ou en finance ("flux" monétaires...).
Références :
Autres liens en vrac à propos des cartes :
L'une des très grandes qualités de cet ouvrage (hormis sa présentation très claire et agréable) se cache derrière la méthode employée pour la génération de ses cartes. En effet, il s'agit d'une méthode numérique récente (2004) développée par Michael Gastner et Mark Newman (coauteur de l'ouvrage et chercheur numéricien à l'université du Michigan).
Cette méthode se base sur le phénomène physique de la diffusion (mécanique des fluides/thermique) : les territoires représentés se déforment comme s'il s'agissait de ballons contenant du gaz (la variable étudiée) avec des zones de pression (les zones de fortes densités de population, le plus souvent). Article de référence : Diffusion-based method for producing density equalizing maps, Michael T. Gastner and M. E. J. Newman (PDF).
D'un point de vue purement numérique, l'équation de la diffusion est résolue par une transformée de Fourrier rapide (FFT) et intégrée par une méthode de Runge-Kutta d'ordre 4. Selon les auteurs, une précision à 1.0E-4 (cela peut paraître décevant, mais une précision plus grande n'est quasiment pas observable humainement) est obtenue en peu d'itérations (ordre de temps de calcul : quelques minutes sur un ordinateur de bureau).
Ce qui m'a paru intéressant dans cette méthode, c'est l'application d'un problème de physique (la diffusion/mécanique des fluides) à un contexte tout à fait décalé (cartographie/représentation des données). Dans l'article cité plus haut, sont listées les précédentes méthodes de génération de cartogrammes, dont une autre consiste en une analogie physique avec l'élasticité des matériaux (mécanique solide déformable).
Dans d'autres domaines, pour ce type d'analogie, on peut citer l'utilisation de méthodes de CFD (calcul en mécanique des fluides) dans des calculs de trafic (routier ou autre) ou en finance ("flux" monétaires...).
Références :
- Atlas du monde réel
- Diffusion-based method for producing density equalizing maps
- WorldMapper
- Mark Newman
Autres liens en vrac à propos des cartes :
Note : le cartogramme présenté ci-dessus est tiré de l'"Atlas du monde réel" et appartient à ses auteurs.


3 commentaires:
outre le fait que ton Atlas me parait bien sympathique et, indeed, utile (citation de mon prof de Zootechnie quand on lui demandait quels bouquins acheter pour compléter son cours, il répondait avec un sourire en coin : "un dictionnaire de langue française et un atlas"), ça me rappelle un peu le phénomène "Spot": c'est super joli!
de l'Ars Numericus...
Salut.
Quand tu dis :
> Ce qui m'a paru intéressant dans cette > méthode, c'est l'application d'un
> problème de physique (la
> diffusion/mécanique des fluides) à un
> contexte tout à fait décalé
> (cartographie/représentation des données
Tu sais que les mathématiques étaient très liés à la géographie, matières qui semblent aujourd'hui très éloignés :d ?
Par exemple, Erathostène a écrit le premier livre de géographie.
Sinon, bon article, je m'en vais lire les autres.
@ Lefty :
Oui, effectivement, j'ai pas insisté là-dessus, mais c'est assez esthétique dans l'ensemble. Le bouquin a vraiment un design agréable en plus...
@ Anonyme :
Tout à fait. C'est d'autant plus vrai qu'à l'époque, les méthodes de cartographie reposaient bien sûr sur la géométrie, mais aussi sur l'astronomie pour les mesures (estimation plutôt) de distances.
Ce que je voulais dire dans ce passage, c'est que c'est assez surprenant, c'est de dire : "Regardez cette méthode de simulation d'écoulement, je l'applique à une génération de carte.". C'est plus sur l'origine "physique" de la méthode que sur son côté purement mathématique.
Enregistrer un commentaire